Materi ajar Lingkaran
Sebelum membahas materi yang lebih spesifik, terlebih dahulu kita ingat – ingat dan harus tahu bagian – bagian lingkaran itu sendiri dan apa itu definisi lingkaran.
Definisi lingkaran sebagai berikut ini :
“Circle is defined as the set of points in a plane that a fixed distance, called the radius, from some fixed point
, called the center” (Encyclopedia of Mathematics, James Tanton, PH.D,2005)
Kurang lebih artinya begini, lingkaran didefinisikan sebagai himpunan titik – titik pada bidang datar yang memiliki jarak  , yang kemudian disebut sebagai jari – jari, dari suatu titik
, yang kemudian disebut sebagai jari – jari, dari suatu titik 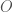 yang disebut titik pusat. Nah, difahami ya kalimat tersebut, kalau belum faham, silahkan ditanyakan kepada yang lebih faham.
yang disebut titik pusat. Nah, difahami ya kalimat tersebut, kalau belum faham, silahkan ditanyakan kepada yang lebih faham. 
Definisi sudah, nah selanjutnya, kita perlu tahu juga bagian – bagian dari lingkaran itu sendiri, dari definisi saja kita sudah tahu istilah jari – jari dan titik pusat. Perhatikan gambar berikut ini :
- Titik
disebut titik pusat
dinamakan jari – jari, biasanya dinotasikan dengan
yang kepanjangannya adalah
dan artinya jarak.
merupakan diameter yang juga sering dinotasikan menggunakan
.
adalah busur lingkaran, biasanya ada yang menggunakan notasi seperti ini
untuk busur
.
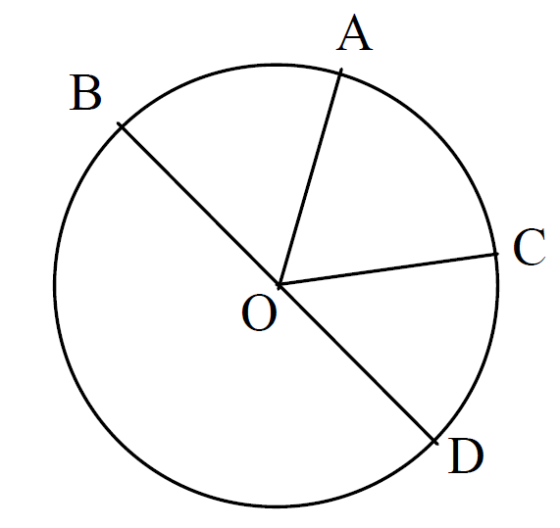
Nah sekarang perhatikan gambar berikut ini juga :
- Wilayah yang berwarna merah adalah tembereng.
- Warna biru merupakan juring.
- Garis
merupakann tali busur.
- Nah, jika saya tarik garis lurus dan tegak lurus dari titik
ke garis
, garis tersebut dinamakan apotema.
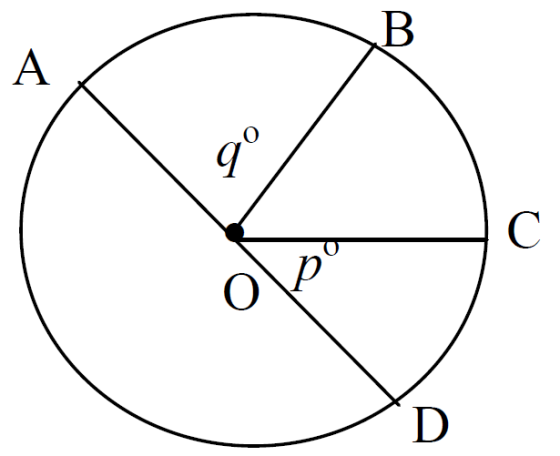
Selanjutnya untuk istilah sudut pada lingkaran :
-
dinamakan sudut pusat lingkaran
. (kenapa kog dinamakan lingkaran
?, karena titik pusatnya namanya
)
- dan untuk
dinamakan sudut keliling.
Oke sudah mengetahui hampir semua bagian dari lingkaran. Selanjutnya kita bahas beberapa rumus – rumus dasarnya :
Luas lingkarandengan
adalah jari – jari lingkaran
Keliling lingkaran, dimana
adalah diameter lingkaran
Ingat :atau
Biasanya, kebanyakan kita masih bingung ketika diberikan soal perbandingan luas dari dua buah lingkaran, yang perlu diperhatikan untuk soal jenis seperti ini adalah bagian lingkaran yang berbeda, yaitu sering kali yang dibandingkan adalah  atau
atau  .
.
Misalkan ada soal seperti ini :
- Diketahui panjang diameter lingkaran
adalah lima kali lebih panjang dari panjang diameter lingkaran
, tentukan perbandingan luas kedua lingkaran tersebut!
Solusi :
1. Misalkan  adalah diameter lingkaran
adalah diameter lingkaran  dan
dan 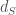 adalah diameter lingkaran
adalah diameter lingkaran  . Jadi, dapat dituliskan sebagai berikut ini :
. Jadi, dapat dituliskan sebagai berikut ini :
Diketahui :
Ditanya :
Perbandingan luas lingkaran … !
Jawab :
Dapat langsung dibentuk menjadi :
Perhitungan di atas ini  saling membagi, sehingga
saling membagi, sehingga 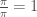 .
.
Perhatikan bahwa pembagian dari dua pecahan cara mengerjakannya dengan mengalikan penyebut yang sudah dibalik, berikut ini caranya :
sehingga diperolehLuas lingkaran  : Luas lingkaran
: Luas lingkaran  .
.
Luas Juring, jika diketahui sudut pembentuk juring adalah(lihat gambar tepat di atas), maka luas juring dirumuskan
atau
Panjang busurdirumuskan dengan
Selanjutnya, berikut ini hubungan antara panjang busur dan luas juring.
Aturan di atas ini sangat penting loh, jadi tolong diingat baik – baik ya. ^_^
Nah, sekarang perhatikan tembereng yang diarsir warna kuning di atas tepat ini, untuk mencari luas tembereng tersebut, kita memerlukan luas segitiga  (warna merah) dan luas juring
(warna merah) dan luas juring  , sehingga rumus mencari luas tembereng adalah :
, sehingga rumus mencari luas tembereng adalah :
Luas Juring – Luas Segitiga =–
Ingat, segitiga yang membentuk selalu sama kaki.
Review lagi :
- Bagian-bagian lingkaran (sudah), yaitu jari – jari, diameter, busur, tali busur, titik pusat, juring, tembereng, sudut pusat, sudut keliling.
- Rumus luas lingkaran (sudah)
- Rumus keliling lingkaran (sudah)
- Rumus luas juring (sudah)
- Rumus luas tembereng (sudah)
- Pembahasan sudut pusat (SP) dan sudut keliling (SK),ini belum. mari kita lanjutkan.
Masih di Materi Lingkaran Lengkap SMP
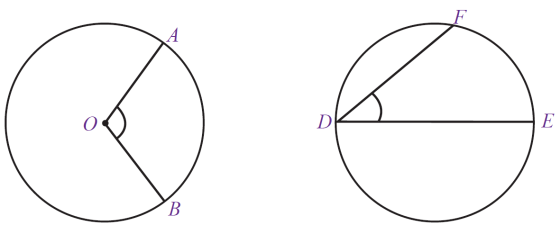
Berikut ini dua gambar lingkaran dengan sudut yang berbeda,
Sebelah kiri adalah sudut pusat dan sebelah kanan adalah sudut keliling, selanjutnya kita bahas rumus-rumus yang berlaku untuk keduanya.
Perhatikan gambar di atas, 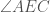 adalah sudut pusat dan
adalah sudut pusat dan  adalah sudut keliling. Kedua sudut tersebut menghadap pada busur yang sama yaitu, busur
adalah sudut keliling. Kedua sudut tersebut menghadap pada busur yang sama yaitu, busur 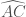 . Nah ketika sudut pusat dan sudut keliling menghadap pada busur yang sama, maka rumus yang berlaku adalah :
. Nah ketika sudut pusat dan sudut keliling menghadap pada busur yang sama, maka rumus yang berlaku adalah :
- Besar sudut pusat adalah dua kali sudut keliling
atau
- Besar dua sudut keliling yang saling berhadapan dan kaki – kaki sudutnya berada pada busur yang sama, maka jumlah kedua sudut keliling tersebut $180^o$
Diingat ya, “Besar sudut pusat adalah dua kali sudut keliling, jika kedua sudut tersebut menghadap pada busur yang sama”.
Misalkan ada soal seperti pada gambar berikut ini :
Berapakah besar  jika besar sudut pusat
jika besar sudut pusat  ?
?
solusi :
Berdasarkan hubungan dari sudut pusat dan sudut keliling, yaitu jika sudut pusat dan sudut keliling menghadap pada busur yang sama, maka besar sudut pusat dua kali besar sudut keliling.
Dari sini sudah jelas bahwa besar  adalah
adalah  , karena besar sudut keliling adalah setengah dari besar sudut pusat.
, karena besar sudut keliling adalah setengah dari besar sudut pusat.
Review :
- Besar sudut pusat dua kali besar sudut keliling jika kedua sudut tersebut menghadap busur yang sama
- Besar dua sudut keliling yang berhadapan adalah
Selanjutnya, yang terakhir.
Sudut antara dua tali busur
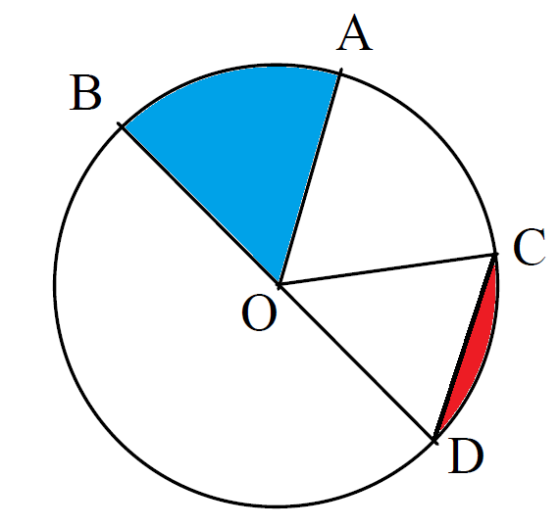
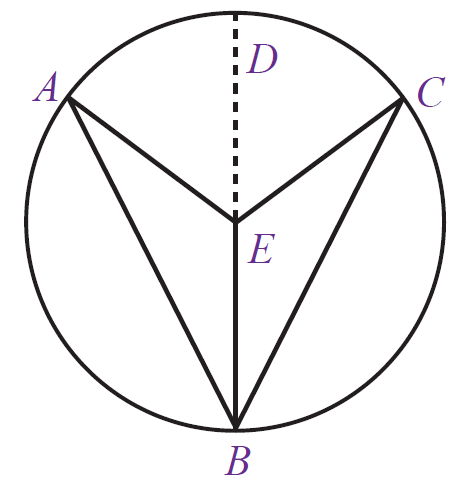
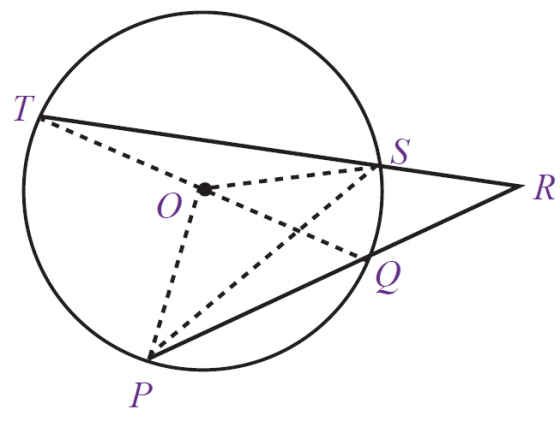
Perhatikan gambar ketiga lingkaran berikut ini :
Ada tiga kasus, kasus yang pertama tali busur berpotongan tepat pada lingkaran (gb.a), tali busur berpotongan didalam lingkaran (gb.b), dan tali busur berpotongan di luar lingkaran (gb.c).
Nah, jika ada soal yang diminta untuk menemukan sudut dengan keadaan salah satu dari ketiga kasus di atas, berikut ini rumus yang kita gunakan :
Untuk kasus (a), ini sudah termasuk yang di bahas di atas, jadi kita lewatkan saja.
Untuk kasus (b), yaitu tali busur berpotonga di dalam lingkaran.
Rumus yang kita gunakan adalah
Untuk kasus (c), perpotongan tali busur berada di luar lingkaran.
Rumus yang digunakan adalah sebagai berikut ini :











Tidak ada komentar